JEE 2015 :: Main 2015 :: Physics 2015

• Main 2015 - Physics 2015
• Main 2015 - Chemistry 2015
• Main 2015 - Mathematics 2015

On a hot summer night, the refractive index of air is smallest near the ground and increases with height from the ground. When a light beam is directed horizontally, the Huygens principle leads  us to  conclude that as it travels, the light beam

Answer:

Explanation:

 According to snell's law,

             $\mu\sin\theta=Constant$

$\therefore$  $\sin\theta\propto\frac{1}{\mu}$

  As μ  increases   ,θ decreases

  Hence beam will bend upward

A red LED  emits light at 0.1 W uniformly around it. The amplitude  of the electric field  of the light  at a distance of 1m from the diode is

Answer:

Explanation:

Consider the LED  as a point source of light

 Let the power of LED is  P.

 Intensity at r from the source

           $I=\frac{P}{4\pi r^{2}}$  ..........(i)

 As we know that 

            $I=\frac{1}{2}\epsilon_{0} E_{0}^{2}c$              ..........(ii)

 From Eq  (i) and (ii)  , we can write

               $\frac{P}{4\pi r^{2}}=\frac{1}{2}\epsilon_{0} E_{0}^{2}c$

or            $ E_{0}^{2}=\frac{2P}{4\pi\epsilon_{0}r^{2}c}=\frac{2\times0.1\times9\times10^{9}}{1\times3\times 10^{8}}$

     or      $E_{0}^{2}=6\Rightarrow E_{0}=\sqrt{6}=2.45V/m$

An inductor (L=0.03H) and a resistor (R= 0.15kΩ) are connected in series to a battery of 15V EMF in a circuit shown below. The key K₁  has been kept closed for a long time. Then at t=0, K₁   is opened and key K₂ is closed simultaneously. At t=1ms, the current in the circuit will be (e⁵  =150)

Answer:

Explanation:

Central Idea:    After long time inductor behave as short -circuit

  At t=0 , the inductor behaves as short-circuited . The current

              $I_{0}=\frac{E_{0}}{R}=\frac{15V}{0.15kΩ}=100mA$

As K₂   is closed current through the inductor starts decay , which is given at any time t as

     $I=I_{0}e^{\frac{-tR}{L}}= (100mA)e^{\frac{-t\times 15000}{3}}$

At t=1ms

      $I=(100mA)e^{-\frac{1\times 10^{-3}\times15\times 10^{3}}{3}}$

                 $I=(100mA){e^{-5}}=0.6737 mA$

or           I= 0.67 mA

A rectangular loop of sides 10 cm and 5 cm carrying a current I of 12A is placed in different orientations as shown in the figures below.

   If there is a uniform magnetic field of 0.3 T in the positive z-direction in which orientations the loop would be in (i) stable equilibrium and (ii)  unstable equilibrium?

Answer:

Explanation:

Since B is uniform only torque acts on a current-carrying loop.

  As,    $\tau=M\times B$ 

  $\Rightarrow$          $|\tau|=|M||B|\sin\theta$

 For orientation shown in (b)  $\theta=0^{0},\tau=0$

             (stable equilibirum)

  and for (d)  $\theta=\pi,\tau=0$  (unstable equilibium)

Two long current carrying thin wires, both with current I, are held by insulating threads of length L and are in equilibrium as shown in the figure, with threads making an angle θ with the vertical. If wires have mass λ per unit length then, the value of I  is (g= gravitational acceleration)

Answer:

Explanation:

Consider free body diagram of the wire.

 As the wires are in equilibrium, they must carry current in the opposite direction

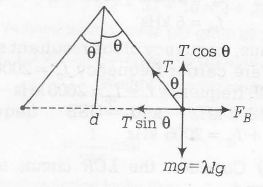
 Here,  $F_{B}=\frac{\mu_{0}I^{2}l}{2\pi d}$, where l is length of each wire and d is separation between wires.

 From figure,   $d=2L \sin\theta$

                $T=\cos\theta=mg=\lambda lg$ (in vertical direction) ......(i)

                      $T \sin\theta=F_{B}=\frac{\mu_{0}I^{2}l}{4\pi L\sin\theta}$

                                         ( in horizontal direction 0   .....(ii)

From Eqs. (i) and (ii)

  $\frac{T \sin\theta}{T\cos\theta}=\frac{\mu_{0}I^{2}l}{4\pi L\sin\theta\times\lambda lg}$

  $\therefore$              $I= \sqrt{\frac{4\pi\lambda L g \sin^{2}\theta}{\mu_{0}\cos\theta}}$

                    $=2\sin\theta \sqrt{\frac{\pi\lambda Lg}{\mu_{0}\cos\theta}}$

• Main 2015 - Physics 2015
• Main 2015 - Chemistry 2015
• Main 2015 - Mathematics 2015